Activity 3: Image Types and Basic Image Enhancement

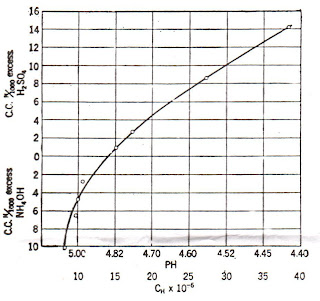
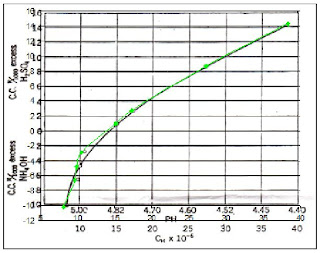
True Color (RGB)

FileSize: 139787
Format: JPEG
Width: 800
Height: 771
Depth: 8
StorageType: truecolor
NumberOfColors: 0
ResolutionUnit: inch
XResolution: 72.000000
YResolution: 72.000000

http://us.fun.marinov.net/store/Village%20Scenery/Village%20Scenery%20-%201.jpg

Indexed

FileSize: 28933
Format: GIF
Width: 500
Height: 344
Depth: 8
StorageType: indexed
NumberOfColors: 8
ResolutionUnit: centimeter
XResolution: 72.000000
YResolution: 72.000000

http://www.wingo.com/opinion/watch_out_kid.gif

Grayscale

FileSize: 97685
Format: JPEG
Width: 450
Height: 342
Depth: 8
StorageType: indexed
NumberOfColors: 256
ResolutionUnit: inch
XResolution: 72.000000
YResolution: 72.00000

http://gsc.nrcan.gc.ca/labs/ebeam/images/sem8.jpg

Binary

FileSize: 38062
Format: BMP
Width: 775
Height: 380
Depth: 8
StorageType: indexed
NumberOfColors: 2
ResolutionUnit: centimeter
XResolution: 118.430000
YResolution: 118.430000

http://baec.tripod.com/AUGUST01/pics/binary_counter.bmp

************************************************
For the second part of the activity, a scanned image was enhanced using the threshold value from the histogram. Thresholding is basically making the region of interest (ROI) of the image well separated from the background. In this activity, a scanned image of a leaf was used.

The image cropped using gimp. The colors were also inverted since I wanted the leaf to be the region of interest. Using scilab, the image was converted to grayscale. Its histogram and image properties were also obtained using the code below. The results then followed.

I=imread("C:\Documents and Settings\mimie\Desktop\leafginv.jpg");
I=im2gray(I);

//histogram
a = 1;
x= [];
y= [];
for i = 0:256
m = find(I== i);
x(a) = i;
y(a) = length(m);
a = a + 1;
end

scf(1)
plot(x,y/max(y)) //end of histogram routine

imshow(I)
imfinfo('C:\Documents and Settings\mimie\Desktop\leafginv.jpg')

Image Properties:
filename: C:\Documents and Settings\mimie\Desktop\leafginv.jpg
filesize:7359
format: jpeg
width: 207
height: 138
depth: 8
storage type: indexed
number of colors: 256
resolution unit: inch
x resolution: 0
y resolution: 0

The histogram of a grayscale image runs from 0 to 255, 0 being black and 255 being white. From the histogram obtained, it can be seen that the ROI (around the second peak) is well separated from the background (the first peak). Also,the threshold value when this image is to be converted into binary is somewhere between 50/255 to 120/255. I used the average [(120+50)/2]/255 as the threshold value and obtained


Converting to binary image (in the command window):

i=im2bw(I,85/255);
imshow(i)

Using the area calculation from 1, the area obtained using Green's theorem, by pixel counting, and the relative error between the two are:

area = 15979
theo = 15978
%error: 0.0062586

To verify the threshold values obtained using scilab, Gimp can be used.

1. Click 'Colors' -->'Threshold' (This will turn the grayscale image into black and white.)
2. Adjust the arrows (or the values) until the ROI is well separated from the background
3. The threshold value for the image is just the minimum/maximum.

Acknowledgemets to Jeric Tugaff for the histogram code (posted in Ma'am Jing's blog) and Ma'am Jing for her suggestions.

I give myself a 9/10 for this activity.

Activity 2: Area Estimation for Images with Defined Edges

For this activity, Green's theorem is used to estimate the area of a binary image with defined edges. The edges of the images were obtained using the "follow" command in Scilab. Area estimation of Green's theorem is
The theoretical value for the area was obtained by counting how many pixels with values of 1.

The code

1 Image=imread("C:\Documents and Settings\mimie\Desktop\hand.bmp"); //read image file
2 I = im2bw(Image,1); //convert image to binary
3
4 [x,y]=follow(I); //get the contour of the image
5 A=[];
6 lx=length(x);
7 ly=length(y);
8
9 //close the contour
10 x(lx + 1)=x(1);
11 y(ly + 1)=y(1);
12
13 for i=2:lx;
14 A(i) = (x(i)*y(i+1))-(x(i+1)*y(i)); //area of the ith triangle
15 end
16
17 Area = (0.5*sum(A)) //Green's Theorem
18 theo = sum(I)
19 err = abs((Area-theo)/theo);
20 %err = 100.*err //percent error



The above code is implemented on the images below:


















with the following results






The error is mainly because of the "follow" command. Since this command is a contour follower, the effective area as estimated by the Green's theorem is lessen by the pixel counts containing the contour. For example a 100x100 square image should have an area of 10000. Using the code above, an area of 9806 is obtained which corresponds to about 99x99 square. This means that the calculation for area starts inside the contour and not at the contour itself. To compensate this, an extra 0.5 lx term is subtracted from the pixel count (line 18: theo = sum(I) - 0.5*lx). The relative error is lessened when this is done.

Raffy and Cherry helped me in this activity. Thank you also to Miguel for troubleshooting the SIP toolbox. For this activity, I give myself a 9/10.

Activity 1: DIGITAL SCANNING

In this activity, ratio and proportion was used to find the numerical values of a digitally scanned plot above. The following steps were followed:

1. The plot was cropped using Paint.
2. Paint was used to find the pixel locations of the data points considered in the plot.
3. MS Excel was used to determine the numerical values in the scanned plot.

• All pixel locations were adjusted such that the pixel location of the origin (121,452) becomes (0,0). Hence all pixel locations of the data points were adjusted using the formula

X = Xpixel - 121
Y = 452 - Ypixel

where Xpixel and Ypixel are the pixel locations of the data points.

• The numerical values were determined using the formula

Xphys = (X*Xp)+5
Yphys = Y*Yp

where Xp = 5/107.1429 and Yp = 2/53.30769 are number of pixels per division in the X and Y axis, respectively.

Note that the +5 in Xphys value is due to the fact that the original plot started at (5,0) and not at (0,0).

The reconstructed plot superimposed with the original plot is shown below:

Notice also that the reconstructed plot has a minimum of -12 instead -10 in its axis. This is because the lowest point in the plot has a y value of less than -10 as can be seen from the original plot. The formula used to get the numerical values are applicable only if the plot considered has axes of equal intervals per division. It can also be used without the +5 offset if the plot considered has an origin at (0,0)

For this activity, I give myself a score of 8/10 since I didn't finish it during class hours. I would also like to acknowledge Janno and Raffy for teaching me how to superimpose the original and reconstructed plots using Open Office and Kaye for her suggestions on offsetting the pixel locations.

The original plot was taken from the book "Outlines of Biochemistry" by Gortner, R. published in 1938. **

**no title page was available from the book