Activity 15: Probabilistic Classification

In this activity, we again classify objects into classes but this time we will use probabilistic classification instead. Specifically, we used Linear Discriminant Analysis or LDA. LDA basically minimizes total error of classification by making the proportion of object that it misclassifies as small as possible [1]. It works by making the features within members of a class near each other and as far as possible to the features of another class. An object is classified into a class where the total error of classification is minimum. As what was done in the previous activity, predetermined features from objects of known classes were used.

Four features were used in this activity. The area and the red, green and blue color from the images. Recall that by using the Euclidian mean, poor classification was obtained for the red feature of the test objects. In this activity, two features are considered for classification. We expect a better classification using this method. The results obtained are as follows:

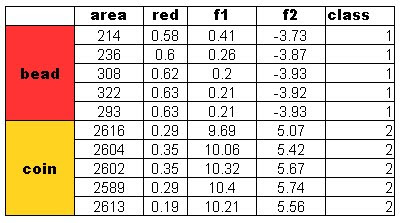A perfect classification resulted from this method and with these features. I tried using the blue and green feature for classification also. Recall from Activity 14 that the green feature gives poor classification and blue gives a perfect classification. The results are:
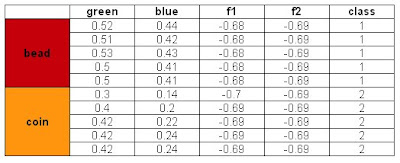Also a perfect classification was obtained. However, when I tried to use the Red and Green feature, the same classification as that in Activity 14 was obtained. We can say that the red and green feature values of the beads and coins are near each other. Hence we cannot classify them perfectly using the said features. To compensate this, we can use a feature that is distinct for each class and combine it with the problematic feature. This is the technique I have used and it worked.

For this activity, I give myself a 10/10 for this activity for doing it alone and for being able to get a perfect classification.

CODE:
x=[214 0.58 0.54 0.45;
236 0.6 0.56 0.46;
308 0.62 0.56 0.49;
322 0.63 0.56 0.5;
293 0.63 0.56 0.5;
2616 0.29 0.24 0.13;
2604 0.35 0.31 0.14;
2602 0.35 0.31 0.14;
2589 0.29 0.25 0.13;
2613 0.19 0.18 0.09];

test = [247 0.57 0.52 0.44;
208 0.54 0.51 0.42;
192 0.55 0.53 0.43;
194 0.52 0.5 0.41;
193 0.52 0.5 0.41;
2736 0.33 0.3 0.14;
2835 0.43 0.4 0.2;
2904 0.47 0.42 0.22;
2925 0.47 0.42 0.24;
2874 0.45 0.42 0.24];


y=[ 1 1 1 1 1 2 2 2 2 2];
y=y';

x1=x(1:5,:);
x2=x(6:10,:);

mu1 = [sum(x1(:,1))/5 sum(x1(:,2))/5];
mu2 = [sum(x2(:,1))/5 sum(x2(:,2))/5];

mu = [sum(x(:,1))/10 sum(x(:,2))/10];

x1o=[x1(:,1)-mu(:,1) x1(:,2)-mu(:,2)];
x2o=[x2(:,1)-mu(:,1) x2(:,2)-mu(:,2)];

c1 = (x1o'*x1o)/5;
c2 = (x2o'*x2o)/5;

C=(c1*5 + c2*5)/10;
Cinv = inv(C);

p = [1/2; 1/2];

f1=[];
f2=[];

for i = 1:10;
xk = test(i, :);
f1(i) = mu1*C*xk' - 0.5*mu1*C*mu1' + log(p(1));
f2(i) = mu2*C*xk' - 0.5*mu2*C*mu2' + log(p(2));
end

class = f1 - f2;
class(class >= 0) = 1;
class(class < 0) = 2;

Reference:
[1] http://people.revoledu.com/kardi/tutorial/LDA/LDA.html